Fuente:http://www.dolmetsch.com/musictheory16.htm
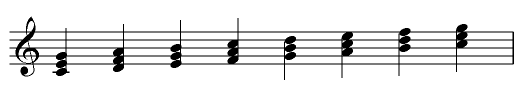

Triads
We examined intervals in an earlier lesson. Intervals are always made up of two notes. We now want to discuss 'chords' and, particularly, chords made up of three notes chosen in a particular way. These 'chords' are called triads. The triad is made up of the root, which is the lowest note in the chord, together with the 3rd and 5th above it. If the root is one of the degrees of a major or minor scale then the triads are given Roman numerals or names identifying that degree, in the following way:
I (tonic triad), II (supertonic triad), III (mediant triad), IV (subdominant triad), V (dominant triad), VI (submediant triad), VII (leading note triad)
The tonic (I), subdominant (IV) and dominant (V) triads are called primary, the remainder (except that on VII) are called secondary. The triad on VII is diminished and is a discord (although its first inversion is not)
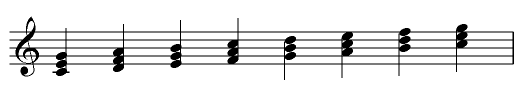
In addition, the triads are classified according to the quality of the 3rd or 5th; i.e. whether diminished (for 3rd or 5th), major (for 3rd), minor (for 3rd) or augmented (for 3rd or 5th).
The notes in a triad can be arranged so that the root is no longer the lowest note of the three. If the 3rd is the lowest note, the triad is said to be a 'first inversion' (using Roman notation, denoted by an additional 'b'; e.g. Vb) and when the 5th is the lowest note, the triad is said to be a 'second inversion' (using Roman notation, denoted by an additional c; e.g. Vc). For completeness, the root position may be denoted by an additional 'a'; e.g. Va.
Triads where all the notes lie in positions closest to the other notes in the chord, are said to be in 'close' position, otherwise the triads are said to be in 'open' position.
Let us now summarise the triad harmonisation of the major and minor scales using numbered chords:

We thank Cedric Debono for helping us correct two misprints in an earlier version of this page.
Notice the 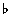 sign in front of III, VI and VII in the natural minor scale. All minor scales are named 'relative' to the major scale on the same key-note. The use of accidental signs in front of numbered chords should be understood to refer to 'raising' or 'lowering' notes in the chord and not necessarily the use of a 'sharp' or 'flat' sign to achieve this. So a 'sharpened' B flat becomes B natural, i.e. 'raised' or 'sharpened' by a semitone.
sign in front of III, VI and VII in the natural minor scale. All minor scales are named 'relative' to the major scale on the same key-note. The use of accidental signs in front of numbered chords should be understood to refer to 'raising' or 'lowering' notes in the chord and not necessarily the use of a 'sharp' or 'flat' sign to achieve this. So a 'sharpened' B flat becomes B natural, i.e. 'raised' or 'sharpened' by a semitone.
There is one further important point that should be noted. In the major, harmonic minor and melodic minor scales above the triad on the dominants are major (the third is a B natural). The B natural is the leading note to the tonic C and this is the most important factor in the dominant fifth wanting to move to a triad or chord of the tonic. In the natural minor, the dominant triad is minor (the third is a B flat) and the pull to the tonic is much weaker. Only when the third is a major third is the triad on the fifth adominant triad.

No hay comentarios:
Publicar un comentario